인공지능 관련 공부를 하거나 논문을 보면 기본적으로 항상 등장하는 개념으로 loss function(손실함수)와 cross entropy 등이 있습니다.
무엇인지 어렴풋이는 알아도 정확하게 자세히 알고 있지 않다면 이 글을 참고하시기 바랍니다.
Entropy 엔트로피
Entropy라는 것은 불확실성(uncertainty)에 대한 척도다. 즉, 엔트로피를 이용해서 불확실성을 줄이고자 하는 것이다.
가장 대표적인 예시로 가방에서 공 꺼내기이다. 공 안에 빨간공으로만 가득하다면 엔트로피=0이다. 불확실성을 신경 쓸 필요가 없다 이 경우엔. 하지만 만약 검은공과 빨간공이 절반씩 담겨있다면 엔트로피는 log(2)=0.69다. 사건 개수가 n이라면 entropy는 log(n)이다. 이 경우엔 entropy가 크다고 말할 수 있다. 하지만 빨간공과 검은공이 다른 비율로 담겨 있는 경우에는 계산을 달리해야겠죠.
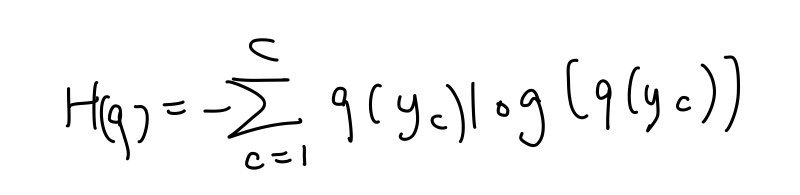
C는 범주 개수, q는 사건의 확률질량함수다.
빨간공이 40%, 검은공이 60%라면,
H(q)=-(0.4log(0.4)+0.6log(0.6))=0.292이다.
빨간공이 90%, 검은공이 10%라면,
H(g)=-(0.9log(0.9)+0.1log(0.1))=0.145 이다.
후자가 엔트로피가 줄어들었다. 예측하기 쉬워지면 엔트로피는 낮아진다.
Cross Entropy 크로스 엔트로피
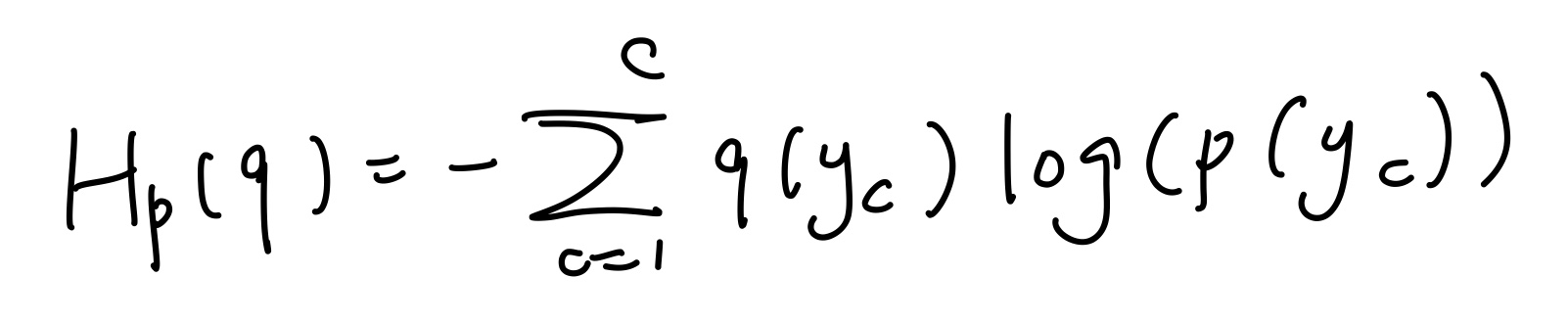
실제 분포를 q라고 정하고, 예측 분포를 p라고 하였다.
머신러닝 예측 모형에서 p분포를 모델링하여 q분포를 예측한다.
q와 p 모두 사용해서 “크로스”를 붙여서 크로스 엔트로피라고 부른다.
엔트로피와는 다르게 실제값과 예측값의 차이(dissimilarity)를 구하는 등 더 상위개념이라고 볼 수 있다.
마찬가지로 공 꺼내기 예시를 들면
빨간공 검은공이 실제로는 0.4% 0.6%분포지만
예측값은 0.3% 0.7%라고 하자.
Entropy값: H(q)=-(0.4log(0.4) + 0.6log(0.6))=0.292
CrossEntropy값: Hp(q)=-(0.3log(0.3)+0.7log(0.7))=0.261
Kullback-Leibler Divergence(KL Divergence)
앞서 설명했던 예측값과 실제값의 차이인 dissimilarity를 측정하는 척도다.
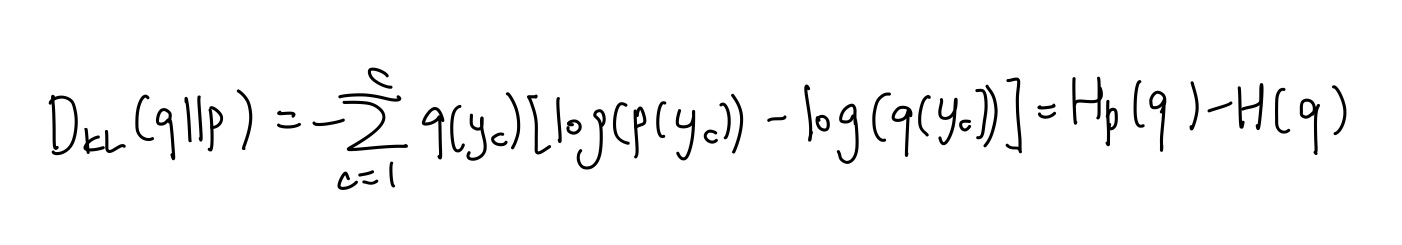
예측값인 cross-entropy는 실제값 entropy보다 항상 크기 때문에 KL Divergence는 항상 0보다 큰 양수값이다. p와 q의 차이를 최대한 줄이는 것, 즉 KL Divergence를 0에 가깝게 하는 것이 머신러닝 예측모형 모델링의 목표이다. 즉 불확실성을 최대한 줄이는 것이다.
Cross-Entropy 적용
머신러닝에서 공 이미지가 있을 때, 그 공이 빨간공인지 검은공인지 하얀공인지 예측을 해본다고 하자.
순서대로 예측 분포를 p(y)=[0.2, 0.3, 0.5]로 모델링하였다.
실제분포가 q(y)=[0, 0, 1]다. 즉, 하얀공이 정답이다. 실제 머신러닝에서는 100%확률을 가진 정답이 존재하기 때문에, [0, 0, 1]이나 [1, 0, 0]과 같은 one-hot encoding된 벡터 형태로 실제분포가 이루어진다. 즉 entropy값은 0이다.
이 경우에는 cross-entropy는 쉽게 -log(0.5)로 계산된다.
그리고 n개의 데이터로 cross-entropy 평균 구하는 식은 다음과 같다.
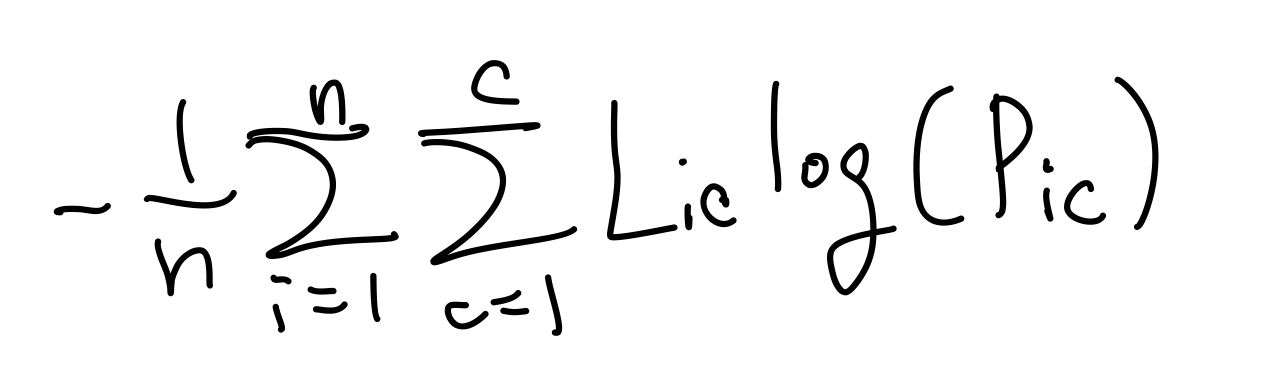
'인공지능 AI' 카테고리의 다른 글
| [인공지능/AI/NLP/자연어처리]BERT Neural Network 언어모델 쉽고 간단한 설명 (0) | 2021.04.23 |
|---|---|
| [인공지능/AI] Hyperparameter Tuning (Optimization) 하이퍼파라미터 튜닝 (최적화) (0) | 2021.04.13 |
| [인공지능/딥러닝/AI] CNN 아키텍처기반의 MNIST 수행하기 (0) | 2020.08.26 |
| [인공지능/딥러닝/AI] 합성곱 신경망 CNN(Convolutional Neural Network) (0) | 2020.08.26 |
| [인공지능/AI]텐서플로를 이용한 MNIST 딥러닝학습 (0) | 2020.08.26 |
