Prototypical Representation Learning for Relation Extraction
ICLR 2021 논문으로
칭화대와 알리바바 작성 논문입니다.
논문에 대해 다루기 전에,
우선 알아야 하는 개념 몇개를 보겠습니다.
Prototype 이란?
일종의 대표값입니다.
우리가 학습을 대규모의 데이터에서 학습을 해야 성능이 좋은데, 보통 이런 여건이 되는 경우는 흔치 않죠..ㅠ
그래서 적은 데이터로도, 학습한 적 없는 데이터에도 좋은 성능으로 결과를 내기 위한 메타 러닝 기법입니다!

k-mean clustering 과정처럼 접근하면 됩니다.
각각 가까운 거리에 있는 점끼리 클러스터링하면 그림과 같이 다른 색깔의 클래스로 군집화가 됩니다.
그러면 그 점들끼리의 평균을 구해서 계속해서 업데이트 작업을 합니다.
그 평균값이 바로 대표값이 되는 겁니다.
즉 하나의 클래스의 'prototype'이 되는거죠!
Prototype for Relation Extraction
해당 논문은 자연어처리의 관계추출 task를 위한 prototyping에 대한 논문입니다.

위에서 다룬 k-means clusteering처럼 각 관계 label(=class)에 클러스터링해서 레이블링을 합니다.
여기선 intra-class compactness and inter-class separability를 다룹니다.
기존의 cross-entropy loss 계산과 다르게, 이 논문은 오직 instance-level supervision만 다룹니다.
따라서 노이즈 제거도 따로 해줍니다.
(다른 클래스에 있는 다른 instance의 feature와 비슷할 경우 mislabeld 될 확률이 크기 때문에 노이즈가 아마 많을거기 때문입니다.)
전체적으로 pretraining fine-tuning 패러다임으로 진행합니다.
1. large-scale distantly labeled dataset에서의 prototype으로 relation encoder를 pretrain
2. 다양한 relational learning settings으로 target dataset에 fine-tune
이렇게 단계가 진행합니다.
2단계에 해당하는 settings에는 이 논문은 각각 supervised, few-shot, and zero-shot settings에서 실험을 진행했습니다.
그리고 추가적으로
probing dataset인 FuzzyRED dataset을 소개합니다. (섹션4.3)
문맥의 이면에 숨겨진 semantics, statement를 찾아주기 위한 데이터라고 합니다.
METHOD
사전에 말했듯이 이 논문은 pretraining-finetuning paradigm으로 따라갑니다.
1단계
large-scale distantly labeled dataset에서의 prototype으로 relation encoder를 pretrain
수식(1)
large-scale distantly labeled dataset는
(w,r) training pair를 가지고 있으며 w는 문장, r는 관계
w = [w1, ..., wn] 이렇게 생겼으며 entities [h, t] 가 마킹되어있습니다.
h는 head, t는 tail로

r은 h와 t의 관계를 정의하며, discrete label로 노이즈가 많을 확률이 큽니다. (추후에 노이즈제거 작업을 또 해줌)

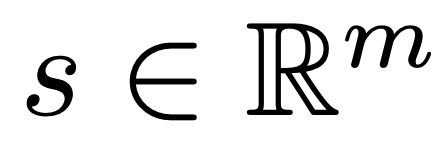
pretrain된 결과값 s는 m차원의 R벡터공간에 매핑됩니다.
수식(2)
z는 prototype로 각 relation인 r을 가집니다.
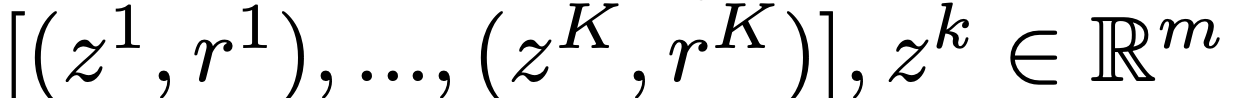
각 K개의 클래스를 가지는 집합을 정의합니다. z인 support set도 m차원의 R벡터공간에 매핑합니다.

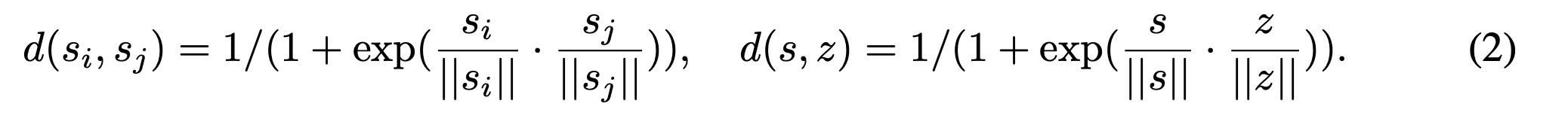
d(si,sj)는 "n-shot"에 해당하는 n개의 support set 중에서 두 statement embeddings 사이의 similarity metric.
d(s,z)는 'n개의 support set 중에서 한 개의 statement embeddings'와 'prototype z' 사이의 similarity metric.
(즉 s^n <--> z^k 의 거리를 구하는 것)
(논문에는 안 써있지만 이런 계산을 하면 비용은 n*k로 계산될 것 같다.)
거리를 계산하는 식인데 왜 지수를 취하고 역수를 취했는지 기하학적 해석은
"angles of the normalized embeddings restricted in a unit ball"에 따랐다고 합니다.
수식(3)

si와 sj가 같은 relation이면 1 (close)
다른 relation이면 0 (dispersed).
intra-class compactness 와 inter-class separability를 보여주는 수식입니다.
또한 positive한 sample을 나머지 negative samples와 대조해서, negative pairs에 더 많은 가중치를 둡니다.
수식(3) 구현 코드
negative_part = torch.sum(repeat_p_rel_emb * repeat_n_rel_emb, -1) / 100 # (batch_size, sample_size)
reversed_p_relation_embedding = torch.index_select(p_relation_embedding.view(1, -1, config['embedding_size']), 1, torch.tensor(reversed_index).cuda()).view(-1, config['embedding_size'])
positive_part = torch.sum(p_relation_embedding * reversed_p_relation_embedding, -1) / 100
max_val = torch.max(torch.max(positive_part), torch.max(negative_part))
cp_loss = -torch.log(torch.exp(positive_part - max_val) / (torch.exp(positive_part - max_val) + torch.sum(torch.exp(negative_part - max_val), -1)) + 1e-5)
3.1 LEARNING PROTOTYPES
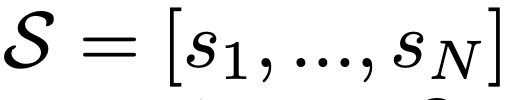
변수 정의:
S^r the subset of all statements si in S with relation r.
S^−r the set of the 나머지 statements.
prototype Z^r for relation r
Z^−r as the set of prototypes z' for all other relations except r.
가정(a):
(a-1) 특정 r <--> r을 가지는 prototype Z^r
(a-2) 특정 r <--> r을 가지지 않는 prototype Z^r
두 거리를 계산했을 때 (a-1)이 (a-2)보다 작아야한다.
가정(b):
(b-1) r을 가지는 prototype Z^r <--> 특정 r
prototype Z^−r <--> 특정 r
두 거리를 계산했을 때 (b-1)이 (b-2)보다 작아야한다.
그리고 각 (a)는 (4), (b)는 (5) 식에 상응한다.
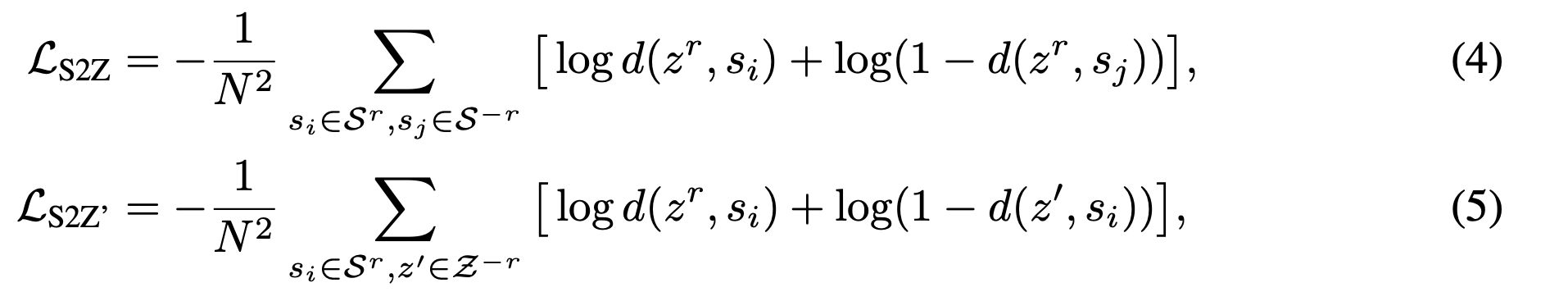
일반적인 cross-entropy loss와의 차이점:
일반적인 cross-entropy loss는 interaction을 고려하지 않지만,
해당 논문의 loss function은 statements and prototypes 사이의 거리를 계산하며 interaction을 고려합니다.
벡터공간에 대한 geometric explanation:
서로 다른 원형 벡터는 가능한 한 큰 각도로 균일하게 분산될 것입니다.
K-disjoint manifolds를 그림으로 나타내면

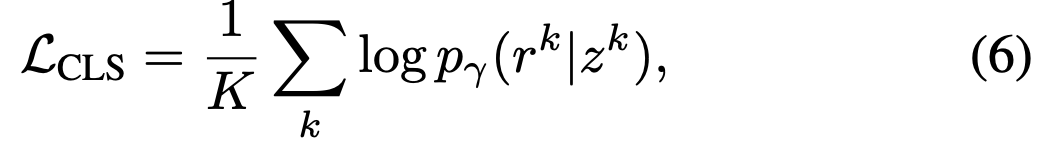
수식(6)은 정규화 과정을 더 거친후에 loss를 minimize한 objective function입니다.
수식(4)(5)(6) 구현 코드
...
p_mlm_loss, p_relation_embedding = bert_encoder(p_input_ids.cuda(), p_e_pos1.cuda(), p_e_pos2.cuda(), attention_mask = p_mask.cuda(), masked_input_ids = p_masked_input_ids.cuda(), masked_lm_labels = p_masked_mlm_labels.cuda())
p_similarity, p_predict_relation = proto_sim_model(p_relation_embedding, p_labels.cuda())
...
n_mlm_loss, n_relation_embedding = bert_encoder(n_input_ids.cuda(), n_e_pos1.cuda(), n_e_pos2.cuda(), attention_mask = n_mask.cuda(), masked_input_ids = n_masked_input_ids.cuda(), masked_lm_labels = n_masked_mlm_labels.cuda())
n_similarity, n_predict_relation = proto_sim_model(n_relation_embedding, p_labels.cuda())
cluster_loss = -(torch.mean(torch.log(p_similarity + 1e-5)) + torch.mean(torch.log(1-n_similarity + 1e-5)))
cls_loss = torch.mean(cross_entropy(p_predict_relation, p_labels.cuda()) + cross_entropy(n_predict_relation, p_labels.cuda())) * 0.5
mlm_loss = p_mlm_loss.mean() + n_mlm_loss.mean()
수식(7)은 노이즈를 분리하는 아이입니다.
샘플간 + 샘플-centroid + 샘플-CLS
마찬가지로 거리에 대한 loss function입니다.
3.2 FINE-TUNING ON DIFFERENT LEARNING SETTINGS
이제 pretraining fine-tuning 패러다임에서
1. large-scale distantly labeled dataset에서의 prototype으로 relation encoder를 pretrain
2. 다양한 relational learning settings으로 target dataset에 fine-tune
2단계 진행합니다.
(a) supervised; (b) few-shot settings
(a) supervised

일반적인 cross-entropy loss으로 feed-forward층에 넣어서 finetuning 진행합니다.
(b) few-shot

(a)와 다르게 input을 정의합니다.


그래서

S*로 정의합니다.
학습(train):
각 다른 prototypes로의 평균 거리를 구해서 feed-forward classifier에 넣고,
cross-entropy loss로 학습합니다.
테스트(test):

input 문장인 query set의 q를 relation r*로 분류하는 작업입니다.
minimum similarity metrics를 구하는 것은 similarity scores의 argmax를 구하는 것과 유사합니다.
아무튼, 이런 메소드로 training set없이도 높은 성능을 보였다는 것이 논문의 전개입니다
